在上篇文章中研究了回歸與分類的問題後，現在讓我們來進入ML簡史，綜觀機器學習的歷史吧!

回歸的起源

回歸(regression)這個詞最早是由法蘭西斯·高爾頓爵士(Sir Francis Galton)，一位英國的人類學家所提出的(雖然跟目前的定義有所不同)。

法蘭西斯·高爾頓爵士(Sir Francis Galton)正在凝視著你

順代一提，他同時也是生物學家達爾文的表弟。他在研究包含豌豆(跟孟德爾一樣，大家都喜歡研究豌豆)等物種父代與子代大小的相關性時，發現體型較大的父代，其子代也會較大，但具體大了多少則不得而知。根據他的研究，子代的比例差距會小於父代的比例，也就是更趨近於均值。例如說父代體型跟均值差了1.5個標準差，則他預測子代體型與均值差距會小於1.5個標準差。經過一代又一代的演化，世代中的變異會倒退而回歸到均值(也就是regress)。姑且不討論這是不是符合目前的理論，我們可以看到這張他在1877年做出世界上第一張線性回歸(linear regression)。

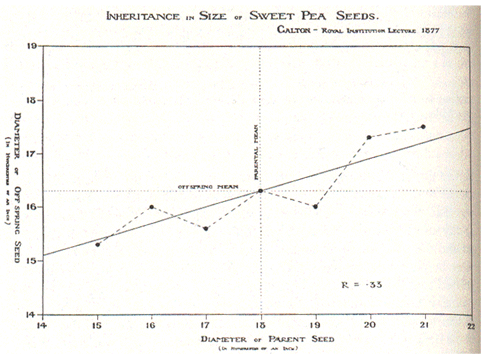
1800年代時算力十分受限，所以當時的人們並沒有意識到這線性回歸在大數據中依然能夠運作得很好。此外，除了回歸分析，梯度下降法(gradient descent method)也能有很好的結果，兩者各有優缺。

線性回歸的數學時間

接著，讓我們來進一步的探討線性回歸

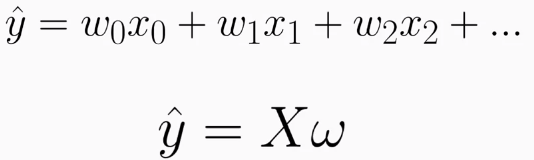
在一個模型中，我們的預測值事實上就是所有權重與向量乘積的總和(這不只在回歸，在深度神經網路一樣適用，後面會講到)。而我們的目標就是找到一個固定的權重值適用於我們的數據集。但我們要如呵判斷所找到的權重的好壞呢?這時就需要用到損失函數(loss function)

損失函數(loss function)

損失函數是深度學習中非常重要的概念，其本質為最佳化理論中的目標函數(objection function)，而好的模型的目標就是將損失函數。

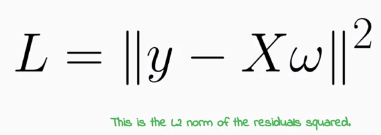
我們可以看到均方差(MSE)作為一種損失函數，公式如上。(待更)

若是覺得本文有幫助，歡迎點選Like、星星收藏或是追蹤系列文支持哦！